April 6, 2016
The Rise of Machine Learning in the Age of Data
“Machine learning is a core, transformative way by which we’re rethinking everything we’re doing.” -Google CEO Sundar Pichai
During the last 10 years, we have been observing the democratization of computing power. The tipping point of this evolution was the accessibility of cloud computing. It started somewhere in 2006 when Amazon launched its Elastic Compute Cloud (EC2) and Simple Storage Service (S3) as a commercial web service, which was the first accessible cloud computing infrastructure service that allowed small companies to “rent computers” on which to run their own applications. Cloud computing is already ubiquitous, and it has definitively changed the IT sector and the way we think IT infrastructure – not only for new businesses, but also for established major players.
This accessibility of computing power, together with the rise of mobile and social and the spread of internet connectivity, lead to the next major hype: Big Data. Big data is characterized by three main features: volume – huge data amount, velocity – speed of data creation, and variety – variety of source. The cloud not only enabled a new service delivery model, but also the way we do data management.
The new reality pushed the appearance of new tools to deal with the enormous amount of data and complexity. Hadoop and later Spark set the base for a new way we deal with Big Data Analytics.
These new algorithms, tools, and affordable computing power are unlocking the potential of data, leading to the next phase: Machine Learning. This is not a new topic. Just like the concepts of cloud computing and big data, machine learning has a long history in computer science and statistics, but only recently have we had all the ingredients for the perfect storm. The technology that was limited to university research or the big players is now available to the public to be incorporated in a wider range of products.
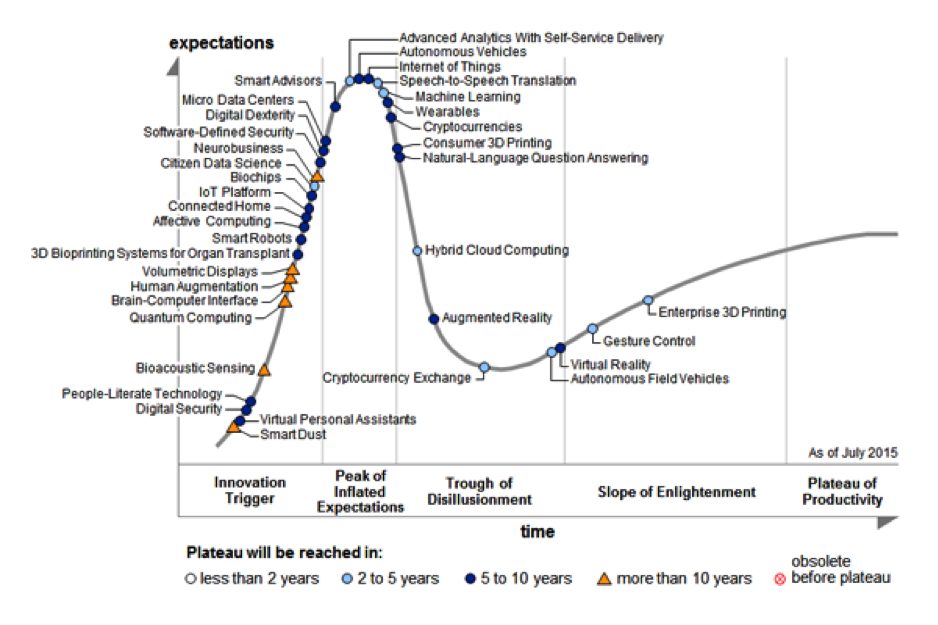
For the first time, Machine Learning was introduced in 2015 in Gartner’s Hype Cycle for Emerging Technologies, directly with a plateau of 2 to 5 years:
Amazon, Google, and Microsoft offer Machine Learning as a service for businesses to explore and derive more meaning out of their data. The algorithms and tools behind their complex systems are now available to be used and applied by any individual or small organization to build more powerful applications.
Microsoft offers Cortana Analytics which “is a fully managed big data management and advanced analytics suite that enables you to transform your data into intelligent action.” It includes a powerful machine learning and Hadoop-based advanced analytics for driving action in real time. It is intended to help organizations predict outcomes and prescribe decisions.
Amazon launched Machine Learning, which is described as “a service that makes it easy for developers of all skill levels to use machine learning technology. Amazon Machine Learning provides visualization tools and wizards that guide you through the process of creating machine learning (ML) models without having to learn complex ML algorithms and technology. Once your models are ready, Amazon Machine Learning makes it easy to obtain predictions for your application using simple APIs, without having to implement custom prediction generation code, or manage any infrastructure.”
Google launched TensorFlow Serving, which is described as “a flexible, high-performance serving system for machine learning models, designed for production environments. TensorFlow Serving makes it easy to deploy new algorithms and experiments, while keeping the same server architecture and APIs. TensorFlow Serving provides out-of-the-box integration with TensorFlow models, but can be easily extended to serve other types of models and data.”
In addition to these platforms from the big players, tools and libraries have come out of academia to the public domain that aid in studying and building methods for data management. The notable mentions are:
- R statistical environment
- Python and libraries such as PAndas, Scikit Learn, SciPy, NumPy
- Weka library
- Apache Mahout
- D3js (data visualization)
The stage is set and everybody wants to be on it. According to Forrester, “Data services and, in particular, data management services, are the key investment areas for most organizations. Innovative companies already differentiate themselves by their management and their use of data to generate new products, services, and customer experiences (such as via predictive analytics)” (source one). However, there is a steep learning curve ahead. “While 73% of companies understand the business value of data and aspire to be data-driven, just 29% confirm that they are actually turning data into action” (source two).
Machine Learning is a key part of the evolution of Data Management and has the potential to impact our lives the same way it happened with the availability of cloud computing. I truly believe that the combination of big data (from disparate sources and in unstructured formats) and machine learning will have a huge impact on society.
How are you preparing yourself for incorporating more sophisticated data management services in your products? I would love for us to look into this more.
Sources
- Data Management Services: Spending Trends For 2014
- Forrester’s Q3 2015 Global State Of Strategic Planning, Enterprise Architecture, And PMO Online Survey.